這次的題目對我來說比較 thinkable 呢

一如以往, A 和 B 理論上都可以秒殺的, 不過 B 看漏了 input 可以 < 0 , WA 了一棍

C 是 given 一個 的01 matrix, 要數有幾多個由1圍成的 square , 一個 square 有兩種:

A)

01110
01010
01110

B)

00100
01010
10001
01010
00100

以且那些 square 不能在 edge or corner touch 到其它不屬於果個 square 邊界的 1, 例如

00001
01110
01110
01110
00000


n,m <= 250

D 是 given 一個 undirected graph, 數有幾多個 simple cycle (無self-cycle, 無 repeated edge/node)

|V| <= 19

Solutions

C 最後雖然做唔切, 但諗到個 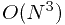的做法

窮舉所有點做一個正方形的左上角, 再窮舉佢的邊長, 用 inclusive-exclusive 快速 check 佢 valid 唔 valid

check type B 的正方形比較麻煩, 不過估計可以將成個 matrix rotate 45度 黎做....

D

一開始諗的是

DP[BIT_PATTERN][X][Y]

BIT PATTERN = 條 path visit 過的 node

X = start node

Y = end node

DP[BIT_PATTERN][X][Y] = number of paths

但單係 state 己經係 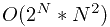, 計埋 transfer 應該會 TLE

之後想到, 這個方法會將一個 cycle 計好幾次, 例如 (1->5->7->2->1) 等價 (5->7->2->1->5) ...

解決方法就係 set 死 node label 最小的 node 為 start node!

所以 state 變為 DP[BIT_PATTERN][Y]

最後一次過加哂 valid 的 DP[BIT_PATTERN][Y] !

不過有個位忘了用 long long, 浪費左唔少時間..

總 time order: