- No Title -
很煩.. 突然又覺得 blogspot 方便好多
始終呢度未成熟同 blogspot 的功能多好多
不過缺點是打 TeX 和 syntaxhiglight 會比較煩 =[
Steiner Tree
Steiner Tree Problem
Given Graph G(V,E) , find a set of edges such that v1, v2, ... vm is connected with minimum cost.
這個是原本的 steinier tree problem.. 本身是 NP 的, 但在 m 很小時, 可以用 DP 去做
由於目標是「連通」,所以果 set edges 一定係一棵 tree , 因為有 cycle 的話 delete 一條 edge 也不破壞其連通性
Step 1) 用 floyd warshall 搵哂 all pairs shortest path
Step 2) 做 DP, state 為 dp[x][1<<m], 代表以 x 為 root 的 tree 去 connect 果 bitset 的 vertex 的 minimum cost
時間複雜度 = 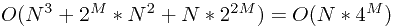
N = |V|
M = 要 connect 的 vertex 的數目
核心算法代碼:
d[n][n] = cost
u[m] = v1, v2, ... vm 的 node label
for (int k=1;k<=n;k++)
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++) d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
for (int i=1;i<=n;i++){
dp[i][0]=0;
for (int j=0;j<m;j++) dp[i][1<<j]=d[i][u[j]];
}
for (int i=1;i<(1<<m);i++){
if ((i&-i)==i) continue;
for (int j=1;j<=n;j++){
dp[j][i]=INF;
for (int k=1;k<i;k++)
if ((i|k)==i) dp[j][i]=min(dp[j][i],dp[j][k]+dp[j][i-k]);
}
for (int j=1;j<=n;j++)
for (int k=1;k<=n;k++) dp[j][i]=min(dp[j][i],dp[k][i]+d[j][k]);
}
註:
(i&-i)==i 是在 check i 的 2進制 是否只得 1 個 1
最後任意一個 dp[u[i]][1<<m] 便是答案
Steiner Tree Problem for specific path
呢個係做題目見到既版本.. 要求不是 v1, v2, ... vm 全部 connect , 而是對數對特定的 vertex 需要被 connect , 如 v1 和 v1', v2 和 v2' 等
係呢個情況, 個 solution 可能唔係一棵 tree, 而是可能由數棵不相交的 tree 組成 (即 forest)
做法大致和原本的 steinier tree 相似, 不過最後不是就咁 return dp[u[i]][1<<m] , 而係要做多次 dp , 睇下點砌d tree 先係 optimal
SRM 470 D1 500
Little John has drawn a rectangle. On the top edge, he draws n dots at different places and numbers them 1 through n from left to right. On the bottom edge, he also draws n dots at different places and numbers them 1 through n from left to right.
John will then draw n straight line segments. For each segment, he will first choose a dot on the top edge that has not been chosen earlier. Then, he will choose a dot on the bottom edge that has not been chosen earlier. Finally, he will connect those two dots to form a straight line segment.
John has drawn several of the n segments so far. You are given vector <int>s startDot and endDot. startDot[i] is the number of the top dot chosen for the i-th segment which has already been drawn, and endDot[i] is the number of the bottom dot chosen for that segment. For each remaining segment, John will randomly choose an available top dot and an available bottom dot (each available top dot has an equal probability of being chosen, and each available bottom dot has an equal probability of being chosen). Return the expected number of distinct pairs of line segments that cross each other in the final drawing.
Google Code Jam 2010 Round 1A
朝早九點開波.. A - "K"子棋, given current state, 問 rotate 90o 後邊一邊會勝出 (可以both/neither) 但開頭 score 分佈出錯左, 以為有 trap, 所以無即刻揼.. 決定睇埋B,C先 B - given sequence C - 兩人玩的game, 一開始有兩個數 (A,B), 每一個 step 可以改為 (A , B-A*k) 或 (A-B*k , A) , k 是正整數, 問某個 range 入面有幾多 pair (A,B) 是 winning state analyze下, B 明顯係 DP, 應該幾輕鬆 ; 但 C 疑似 Nim game 果類, 基本上係未 code 過 之後佢出 clarification 改返分數, 發現 A 佔分最少, 於是放心去寫A, 大約 30 mins 時 A-small Correct! 今次打算用一個 strategy - 唔隊 large 住, 之後有時間再 double check 多次, 因為 large 得一次機會同埋GCJ 計時間係計最後 submission, 對penalty無咩影響 (如果之後會再 submit 的話) 寫 B - DP, change 同 delete 好易 handle, add 諗左一陣, 確定係 round up 除法, 過 test case, Correct! 之後就朝 C 進發 C - 睇多睇又唔似 nim, 於是用 memorization 的方法去打個表搵observation, 得到 很明顯地有 pattern -- 之後就陷入一小時的掙扎 一開始以為係好簡單既 pattern, 但試左幾個 sequence 後後面又總係唔 work, 於是出動武器 - KMP 用電腦去搵 pattern, 但 turns out 佢係無一個 "repeat" 既 component ..! 唔忿氣, 出動埋 guassian , 話唔定係一條 polynomial , 入左頭 5 個數落去就知唔 work - solve 出黎的 coefficient 唔係 integer ... 睇黎條 sequence 唔係 polynomial .. 諗 諗 諗 剩返 20 mins 果陣, 突然發現 - 123456789 每一行/列 * 的數目 等於 果行/列 的篇號! 諗深一層, 其實係同 self-describe sequence 差唔多 突然感覺到離答案只差一步 揼... 揼... 揼... 大約剩返 8 mins 時揼好, submit, Incorrect 灰左一灰, 但立即想到是 BIT 越界問題, 改, Correct! Result ..
![{A_n}, A_i \in [0,255] {A_n}, A_i \in [0,255]](/user_files/gagguy/epics/776c2b795d18f69da649b39ea51a2f0d3f6a140d.png) , 可以 add/delete/change (各自有 cost) , 目標係試 neighbour 的 difference <= M, 求 min cost
, 可以 add/delete/change (各自有 cost) , 目標係試 neighbour 的 difference <= M, 求 min cost
1*........
2.**......
3.***.....
4..****...
5...*****.
6...******
1*........
2.**......
3.***.....
4..****...
5...*****.
6...******

| 113 |
 |
gagguy
Me |
100 | 2:30:38 |   32:50 32:50 |
  1:36:12 1:36:12 |
  50:27 50:27 |
  1:39:01 1:39:01 |
  2:26:02 2:26:02 1 wrong try |
  2:26:38 2:26:38 |
不過最滿足都係做到條 C 後記 睇返 official report, 原來 B 有 GCJ 牽涉的範疇真的很廣泛, 學多d野才是上策
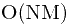 的做法, C 和 golden ratio 有關
的做法, C 和 golden ratio 有關
Code Forces Contest #11
這次的題目對我來說比較 thinkable 呢
一如以往, A 和 B 理論上都可以秒殺的, 不過 B 看漏了 input 可以 < 0 , WA 了一棍
C 是 given 一個  的01 matrix, 要數有幾多個由1圍成的 square , 一個 square 有兩種:
的01 matrix, 要數有幾多個由1圍成的 square , 一個 square 有兩種:
A)
01110
01010
01110
B)
00100
01010
10001
01010
00100
以且那些 square 不能在 edge or corner touch 到其它不屬於果個 square 邊界的 1, 例如
00001
01110
01110
01110
00000
n,m <= 250
D 是 given 一個 undirected graph, 數有幾多個 simple cycle (無self-cycle, 無 repeated edge/node)
|V| <= 19
Solutions
C 最後雖然做唔切, 但諗到個 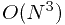 的做法
的做法
窮舉所有點做一個正方形的左上角, 再窮舉佢的邊長, 用 inclusive-exclusive 快速 check 佢 valid 唔 valid
check type B 的正方形比較麻煩, 不過估計可以將成個 matrix rotate 45度 黎做....
D
一開始諗的是
DP[BIT_PATTERN][X][Y]
BIT PATTERN = 條 path visit 過的 node
X = start node
Y = end node
DP[BIT_PATTERN][X][Y] = number of paths
但單係 state 己經係 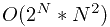 , 計埋 transfer 應該會 TLE
, 計埋 transfer 應該會 TLE
之後想到, 這個方法會將一個 cycle 計好幾次, 例如 (1->5->7->2->1) 等價 (5->7->2->1->5) ...
解決方法就係 set 死 node label 最小的 node 為 start node!
所以 state 變為 DP[BIT_PATTERN][Y]
最後一次過加哂 valid 的 DP[BIT_PATTERN][Y] !
不過有個位忘了用 long long, 浪費左唔少時間..
總 time order: