Steiner Tree Problem

Given Graph G(V,E) , find a set of edges such that v₁, v₂, ... v_m is connected with minimum cost.

這個是原本的 steinier tree problem.. 本身是 NP 的, 但在 m 很小時, 可以用 DP 去做

由於目標是「連通」，所以果 set edges 一定係一棵 tree , 因為有 cycle 的話 delete 一條 edge 也不破壞其連通性

Step 1)  用 floyd warshall 搵哂 all pairs shortest path

Step 2)  做 DP, state 為 dp[x][1<<m], 代表以 x 為 root 的 tree 去 connect 果 bitset 的 vertex 的 minimum cost

時間複雜度 =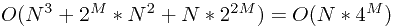 

N = |V|
M = 要 connect 的 vertex 的數目

核心算法代碼:
 

d[n][n] = cost
u[m] = v₁, v₂, ... v_m   的 node label
 

for (int k=1;k<=n;k++)
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++) d[i][j]=min(d[i][j],d[i][k]+d[k][j]);

for (int i=1;i<=n;i++){
	dp[i][0]=0;
    for (int j=0;j<m;j++) dp[i][1<<j]=d[i][u[j]];
}

for (int i=1;i<(1<<m);i++){
	if ((i&-i)==i) continue;
	for (int j=1;j<=n;j++){
		dp[j][i]=INF;
		for (int k=1;k<i;k++)
			if ((i|k)==i) dp[j][i]=min(dp[j][i],dp[j][k]+dp[j][i-k]);
	}
	for (int j=1;j<=n;j++)
		for (int k=1;k<=n;k++) dp[j][i]=min(dp[j][i],dp[k][i]+d[j][k]);
}

註:

(i&-i)==i 是在 check i 的 2進制 是否只得 1 個 1

最後任意一個 dp[u[i]][1<<m] 便是答案

Steiner Tree Problem for specific path

呢個係做題目見到既版本.. 要求不是 v₁, v₂, ... v_m  全部 connect , 而是對數對特定的 vertex 需要被 connect , 如 v₁ 和 v₁', v₂ 和 v₂' 等

係呢個情況, 個 solution 可能唔係一棵 tree, 而是可能由數棵不相交的 tree 組成 (即 forest)

做法大致和原本的 steinier tree 相似, 不過最後不是就咁 return dp[u[i]][1<<m] , 而係要做多次 dp , 睇下點砌d tree 先係 optimal

例子: POJ 3123 Ticket to Ride